1917 Activity: What’s Beyond the Universe?

Einstein was fond of thought experiments. For example, when he was sixteen years old, he imagined what it would be like to travel at the speed of light while holding a mirror in front of him, and asking himself, “will I be able to see my reflection?” Such thought experiments eventually led Einstein to develop his theory of relativity.

You may want to try thought experiment to answers questions that you have about cosmology, for example:

If the universe began with a “bang,” where is the “center” of the universe?

A thought experiment to help you envision an expanding space with no center is to a two-dimensional analogue of the three-dimensional universe. Think about the surface of a perfectly smooth round ball from the viewpoint of an ant crawling on its surface. The ant can travel anywhere on the surface of the ball and find no point that is any more special than anyplace else. The ball could have begun its life as a tiny dot, expanding into a larger and larger sphere, and still there would be no center—just more and more space to crawl around.

Is the universe finite or infinite?

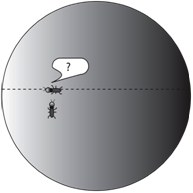This is one of the most important questions asked by cosmologists, and equally difficult to envision. Again the ant crawling on a sphere can be helpful. If the universe is finite, space itself is curved inwards, like the surface of a sphere. Imagine an ant with a will to get somewhere, and instead of crawling around aimlessly sets off in a straight line. On a sufficiently large sphere the surface appears flat to the tiny ant. So it can travel for a very long time, but eventually finds that it has arrived in the same place from which it started!

As three-dimensional beings we can see that the ant just crawled around the sphere. In fact, no matter how far the ant travels it will never reach an edge, and will always end up in the same place. Similarly, if the universe is curved inward, we could travel in a straight line and eventually end up back on our home planet.

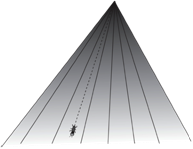An infinite universe, represented by a huge flat sheet, is hard to picture, because it’s difficult for us to imagine any sheet with no edges. In that case the ant who travels in a straight line forever would never return to its starting point, would never find a center, and would never reach an edge. Although the jury is still out, data on the amount of matter in the universe suggests that this is the universe in which we live.

A third possibility is that there is so little matter in the universe it is negatively curved. A way to envision this possibility is to envision a saddle for riding horses. Imagine that the saddle has no edges so that it curves upwards in one direction, and downward in the other direction.

These are just three possibilities. There are many others and many variations to consider. The overall “shape” of the universe continues to be a hot area for cosmological research.