1929 Activity: Age of the Universe

 

Once Hubble and Humason determined the rate at which the universe was expanding and the distances to the galaxies, estimating the age of the universe was straightforward.  As an example, imagine that people are traveling home from a party.  Consider two of the party guests traveling at 50 miles per hour in opposite directions. If they are currently 100 miles apart, how long ago did the party occur? (Place your mouse over the “answer button” to see if you have the answer correct).  
 
 
Similarly, since all of the galaxies are moving apart from each other at measured speeds and at measured distances, it is possible to calculate how long ago they were all together—that must be the age of the universe. 
 
The analogy is not perfect.  The party guests are traveling through space, while in the case of the universe space itself is expanding.  So there is no particular place where the galaxies were all together.  The most common example is a loaf of raisin bread waiting to bake.  As the dough rises the raisins move apart from each other.  Viewed from the perspective of any given raisin, all the other raisin seem to be moving away.  
 
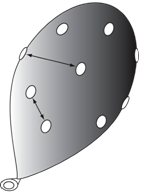You can make a two-dimensional model of the expanding universe without making your own bread.  Take a balloon and blow it up part way.  Glue buttons or other small objects on the balloon with a flexible glue such as rubber cement.  Measure the distance between several of the buttons, and write down the measurements.  Now blow up the balloon further and measure the distances between the buttons again.  Do any of the buttons get closer to each other?  How much do they grow apart?
 
 
A common misunderstanding is that the galaxies are expanding too.  That is not the case.  It is space itself that is expanding, so that the distances between the galaxies are  increasing, not the galaxies themselves. But what about the space between the stars in the galaxies?  If matter is densely compacted and holds itself together, like in galaxies, then the space-time does not expand with the rest of the universe. In the above model the rubber between the buttons represents the fabric of space.  The buttons do not expand, just the distances between them. The gravitational attraction among the stars within a galaxy overcomes the effect of the expansion and keeps the stars and star clusters from drifting apart.